For simulations of dynamics in porous media, we most often end up with one or multiple non-linear systems to solve. Depending on the grid resolution, the systems can be large, and the solution process will often consume a substantial part of the total simulation time. For this reason, research into efficient linear and non-linear solvers is a very active field of research.
The goal of this work package is to design solvers that are tailored to the characteristics of subsurface energy storage. We will consider both methods for non-linear problems, such as fixed-point and Newton’s method, and preconditioners for iterative linear solvers. The coupling of different physical processes (flow, mechanics, temperature) will be handled by iterative coupling schemes, or else block preconditioners.
The development of linear and non-linear solvers has been a long-standing focus for the Porous Media Group. As such, this work package integrates naturally with existing activity in the group, as well as with the other research themes in the TheMSES project.
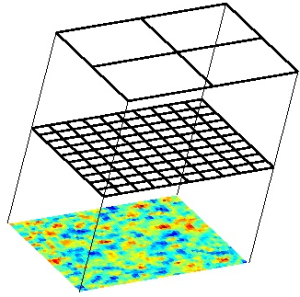
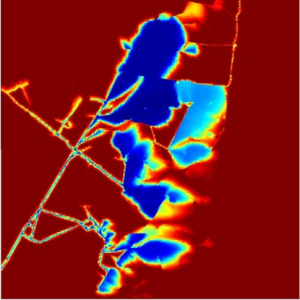
Left: Multi-level grid structure used in linear solvers. Right: Simulation of temperature transport in fractured media using a coarse-scale preconditioner to solve the pressure equation.